In any experiment, randomization is the central criterion necessary to make an inference about cause and effect. This is true whether we are studying inanimate objects, isolated proteins, cells, animals, or people.
Randomization helps us remove the influence of both known and unknown confounders. The ultimate confounders are choice and the passage of time. People (or animals) who choose one thing may be constitutionally different in myriad known and unknown ways from people (or animals) who choose another thing. As a result, “self-selection” or choice acts as a super-confounder. The passage of time also acts as a super-confounder because of its association with a near infinitude of both known and unknown time-dependent trends that can irrevocably mangle our interpretation of any observation if they aren't somehow accounted for. The principle reason that randomization is such a useful tool is that it can account not just for the known confounders but even for those unknown.
The Great Unknown
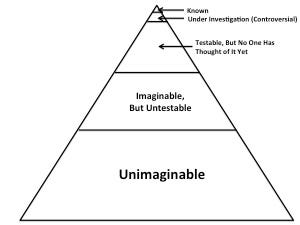
There is unfortunately no way to quantify how much we don't know, but humility, wisdom, and scientific caution all require us to assume that the unknown is likely to vastly exceed the known in breadth, depth, and importance. We can imagine that the total pool of truth looks something like this:
You may have to click on the picture to enlarge it so you can see the tiny space occupied by the “known” portion of truth.
We have probably only begun to investigate a small portion of what can be investigated, and there may be a great deal of truth that is impossible to investigate. Indeed, there may be a great deal of truth that is impossible to even imagine, and there is obviously no way to imagine what such truth might be or just how much of it there is. But that doesn't make it any less true, and doesn't make it any less able to confound our observations.
Epidemiologists study the world around us without performing any experiments. They make observations, which is the critical first step in the scientific method. They establish facts, without establishing cause-and-effect phenomena. Facts are critical.
Epidemiologists also calculate statistical associations between putative causes and putative effects. In so doing, they try to adjust for confounders, but their adjustments necessarily come from the top two layers of truth, things known and controversial things under investigation. Adjustments coming from the second layer, controversial things under current investigation, may simply be wrong, and the adjustments themselves may thus become confounders. Regardless of whether the adjustments improve the analysis in the way they are intended to, scientific caution would require us to assume that the vast majority of counfounders lie in the bottom three layers: things we haven't thought of, things we can't test, and things we can't even imagine.
These are the “unknown unknowns” that Donald Rumsfeld talks about:
Epidemiologists do make some attempt to account for unmeasured confounding, but when doing so they seem to naively assume that any unmeasured confounding is likely to be simple and straightforward. Consider this paragraph from the “Eco-Atkins” paper by Frank Hu, Walter Willett, and other researchers from the Harvard School of Public Health (1):
We also considered the influence of unmeasured confounding by using a sensitivity analysis. We found that for [the Health Professionals' Follow-up Study], the unmeasured confounder would have to have a prevalence of 40% among those at the highest decile of animal score and a [hazard ratio] of 2.0 with total mortality to attenuate the association to nonstatistical significance. In [the Nurses' Health Study], the unmeasured confounder would have a prevalence of 20% and a [hazard ratio] of 2.0 to attenuate the association to nonstatistical significance. Because important confounders for the analyses of total and disease-specific mortality were controlled for, it is unlikely that such strong confounding would remain to explain the observed associations.
I blogged about this study last year in my post, “New Study Shows that Lying About Your Hamburger Intake Prevents Disease and Death When You Eat a Low-Carb Diet High in Carbohydrate.” We can see from the language above that these researchers seem to think they've identified almost everything important already. Thus, they refer not to a potential sea of unknown confounders but “the unmeasured confounder,” and conclude that such a confounder would have to be so prevalent and powerful that it strains the imagination to think it could have escaped their notice.
After all, folks, they're experts! And what expert wouldn't spot such a ginormous confounder? Only an expert that is human, I suppose. One who doesn't know the unknown.
These researchers seem to assume an extremely implausible model of the progress of knowledge, one in which the limit of attainable knowledge is equal to the totality of truth and in which we are rapidly and asymptotically approaching this limit:
There is, of course, no way to disprove such a model at any given moment because we have no way of quantifying what we don't know. Such a model is nevertheless likely to be eternally disprovable in retrospect. We can prove with great confidence, for example, that nineteenth century scientists were not a finger snap away from knowing everything, and people a hundred years from now will likely be able to prove the same about us with just as much confidence. We will never be able to test the untestable or imagine the unimaginable, however, so we will never be able to argue with someone who claims that nothing untestable is true or that nothing unimaginable exists. We nevertheless have the liberty to opt out of foolishness, a liberty for which we should be forever grateful.
The Randomized Experiment
Most experts agree that we should use observational evidence to generate hypotheses about cause-and-effect phenomena, but not to confirm or refute such hypotheses. We use randomized, controlled experiments, by contrast, to support or refute our hypotheses about cause and effect.
It can be easy for us to get hung up on the “controlled” or “experiment” parts and miss the point that the key feature of such an experiment that allows the inference of cause and effect is actually the randomization. To randomize simply means that we start with a group of people (or rats, or rocks, or whatever we are studying) and then randomly allocate the members of this group to one or another treatment to study the effects of that treatment. If all subjects receive two or more treatments and thereby act as “their own controls,” we would randomly allocate them to receive these treatments in different orders.
If the sample size is large enough, randomization ensures that each treatment group is a random sample of the initial group from which it is drawn. If each group is a random sample drawn from the same initial pool of subjects, all of the groups will have a more or less identical pattern of confounding variables, regardless of whether those confounding variables are known to us.
In a small study randomization can sometimes fail to distribute confounders evenly. We can imagine that if we took four people off the street and randomly allocated two of them to group A and two to group B, the two groups might be radically different from one another!
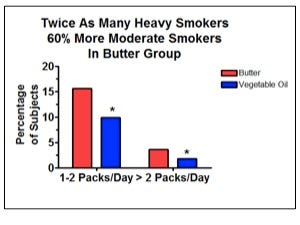
For a more realistic example, the LA Veterans Administration Hospital Study randomly allocated just under 850 men to receive a diet based on butter and other animal fats or a diet based on vegetable oils. I discussed this study at great length in my “Good Fats, Bad Fats” talk at Wise Traditions. The randomization failed to distribute smoking habits evenly, so that there were more moderate and heavy smokers in the animal fat group and more light smokers and non-smokers in the vegetable oil group (2):
This failure makes it more difficult to determine whether any differences between the two groups result from the different diets or from the different smoking habits.
At this point, we should tremble in amazement, realizing we are standing on the brink of an invisible abyss, the ocean of the unknown, full of creatures of confounding great and small. Smoking is a known and rather obvious confounder. If a study with almost a thousand people in it is vulnerable to such an error in the distribution of smoking, are not all studies of this size likely to err in distributing untestable confounders, confounders we haven't thought of yet, and unimaginable confounders?
When small, randomized studies are repeated, however, the likelihood of such failures occurring in a consistent pattern is infinitesimal. And when randomized studies are large enough, the likelihood of such failures even within one study is very low. It is therefore important for us to give greater emphasis to the results of large studies, and to repeat studies so that we can pool their results together and examine a broad totality of evidence.
As C.S. Lewis once wrote (3), “two heads are better than one, not because either is infallible, but because they are unlikely to go wrong in the same direction.”
With scientific studies, this is only true if the error is random. If a study is not randomized properly, error can result from systematic bias, so that repeated studies of the same type are likely to repeat this bias over and over. If the study is properly randomized, the possibility for error is still very great, but such error will be random rather than a result of systematic bias. None of these randomized studies will be infallible, but they are incredibly unlikely to all go wrong in the same direction.
All this said, it would be gross error to say that randomized studies constitute “better” evidence than observational studies. All forms of evidence have their strengths and limitations. The strength of randomized studies is our ability to use them to infer that one thing causes another. This is hardly the only useful type of knowledge.
In future posts, I will elaborate on the “super-confounding” nature of choice and the passage of time, common errors in interpreting randomized studies, the inherent drawbacks of experimental studies, and the value of observational research.
References
1. Fung TT, van Dam RM, Hankinson SE, Stempfer M, Willett WC, Hu FB. Low-carbohydrate diets and all-cause and cause-specific mortality: two cohort studies. Ann Intern Med. 2010;153(5):289-98.
2. Dayton S, Pearce ML, Hashimoto S, Dixon WJ, Tomiyasu U. A Controlled Clinical Trial of a Diet High in Unsaturated Fat in Preventing Complications of Atherosclerosis. Circulation. 1969;150(1 Suppl 2): 1-62.
3. C.S. Lewis, Introduction to the English translation of St. Athanasius the Great's On the Incarnation published by St. Vladimir's Seminary Press, quoted from the 1953 edition.